C++ Binary Search Tree

수성컴전자방입니다. 오늘은 C++로 Binary Search Tree를 만들어 보겠습니다. Binary Search Tree의 왼쪽 자식(left child)의 데이터는 부모 node의 데이터보다 작고, 오른쪽 자식(right child)의 데이터는 부모 node의 데이터보다 큽니다(m_left->data < this->data < m_right->data). 전체 코드는 https://github.com/sooseongcom/BinarySearchTree.git에서 보실 수 있습니다. 원래는 pair로 구현해야 하는데, 이 코드는 제가 공부려고 만든 거라서 그냥 template으로 구현했습니다.

1. 파일 목록

BinarySearchTree.h: Binary Search Tree 관련 class
TreeNode.h: TreeNode class
main.cpp: 테스트를 위한 main 함수

2. Visaul Studio로 컴파일할 때 전처리할 것

_CRT_SECURE_NO_WARNINGS has to be added to preprocessor definitions.

3. insert

template <class T>
void BinarySearchTree<T>::insert(T data) {
	TreeNode<T>* p = m_root, * pp = NULL;	//pp: the parent of p
	while (p) {
		pp = p;
		if (data < p->m_data) p = p->m_left;
		else p = p->m_right;	// data >= p->m_data
	}

	//Perform insertion
	p = new TreeNode<T>(data);
	if (m_root != NULL) {	//tree not empty
		if (data < pp->m_data) pp->m_left = p;
		else pp->m_right = p;	// data >= p->m_data
	}
	else {
		m_root = p;
	}
}

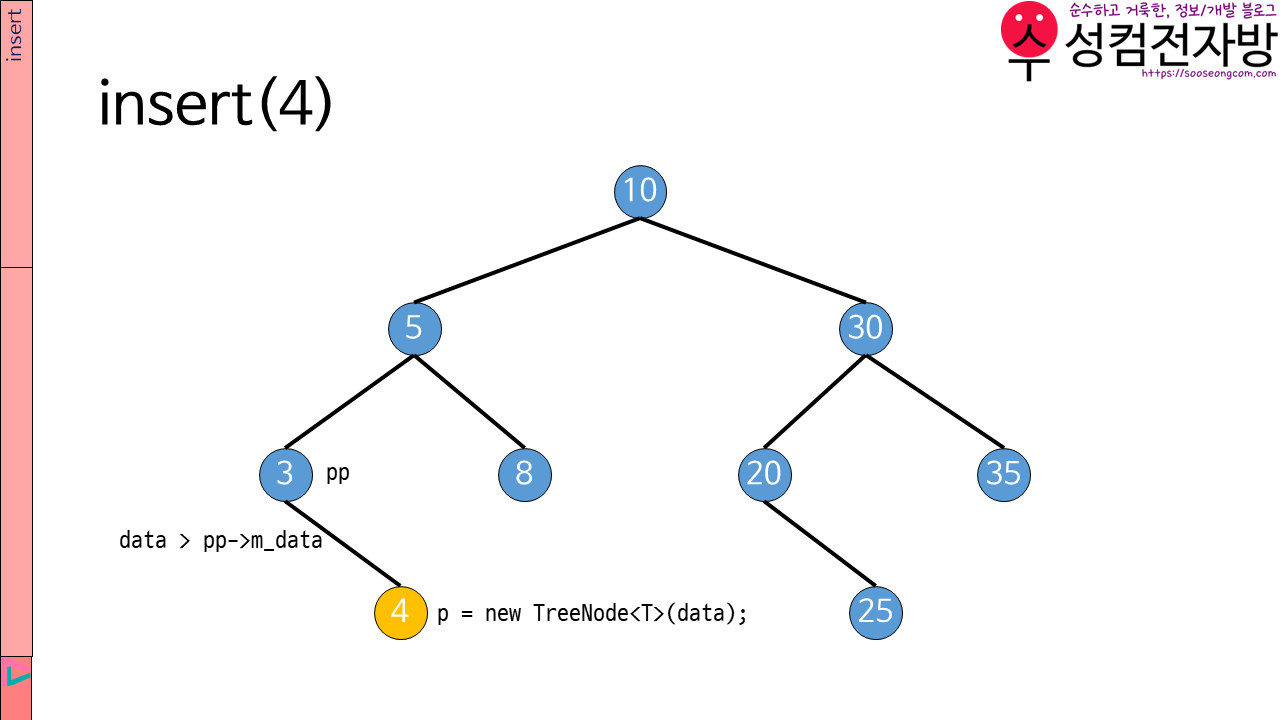
insert
while문(코드블록 기준 4~8행)을 통해 p가 존재하는 동안 자식 node로 계속해서 내려갑니다. Binary Search Tree이기 때문에 숫자의 크기를 비교합니다. p가 존재하지 않게 되면 p에 새 node를 만듭니다.
insert()의 시간 복잡도: O(h). (h: height)

4. delete

template <class T>
void BinarySearchTree<T>::deletion(T data) {
	TreeNode<T>* p = m_root, * pp = NULL;	//p: the node to delete	//pp: the parent of p

	while (p && data != p->m_data) {
		pp = p;
		if (data < p->m_data) p = p->m_left;
		else p = p->m_right;	// data >= p->m_data
	}

p는 삭제할 node이고, pp는 p의 부모 node입니다.
while문(코드블록 기준 4~8행)을 통해 p가 존재하는 동안 자식 node로 계속해서 내려가며 찾는 data와 p->m_data가 같은지 확인합니다.

4.1. not found

if (p == NULL) return;	//(1) not found

p가 없을 경우 함수를 종료합니다.

4.2. if p is a degree 0 node (p is leaf)

if (p->m_left == 0 && p->m_right == 0) {	//(2) p is leaf
    if (pp == 0) m_root = 0;
    else if (pp->m_left == p) pp->m_left = 0;
    else pp->m_right = 0;

    delete p;
    return;
}

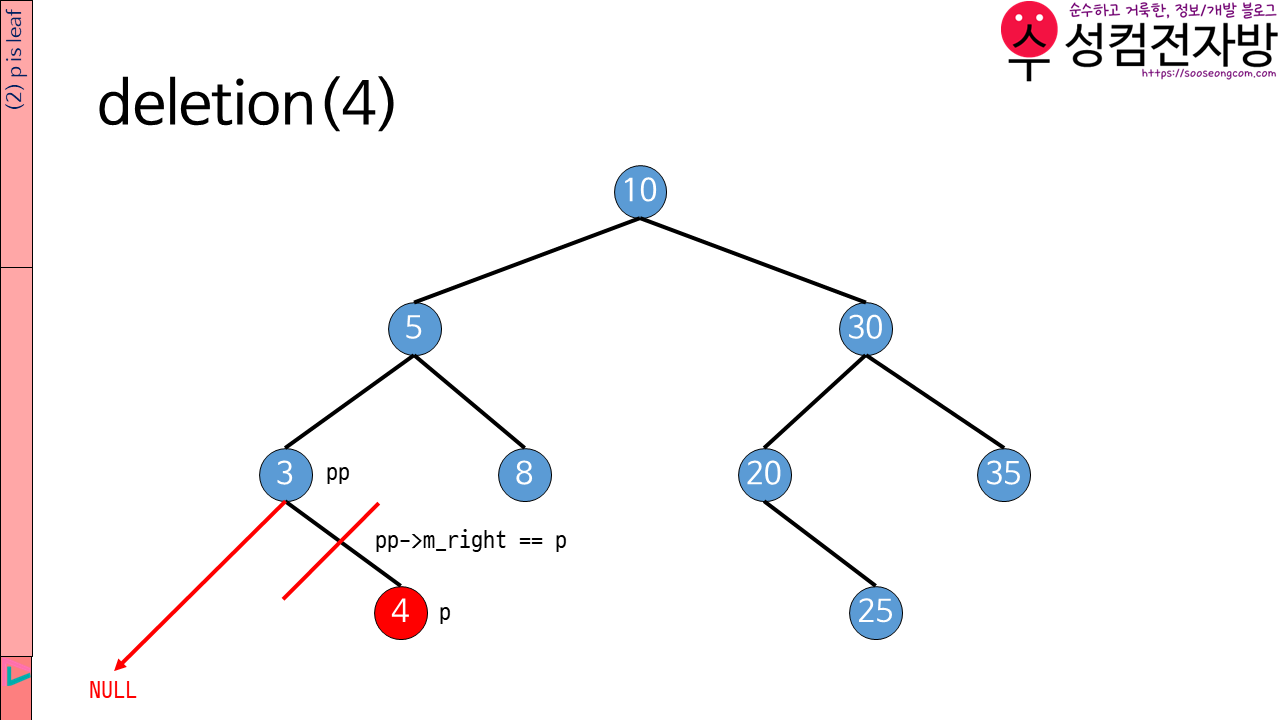
p is leaf
p의 자식 node가 없을 경우 pp->m_left가 p이면 pp->m_left=0;을, pp->m_right가 p이면pp->m_right=0;을 실행합니다.

4.3. if p is a degree 1 node

if (p->m_left == 0) {	//(3-1) p has only right child
    if (pp == 0) m_root = p->m_right;
    else if (pp->m_left == p) pp->m_left = p->m_right;
    else pp->m_right = p->m_right;

    delete p;
    return;
}

if (p->m_right == 0) {	//(3-2) p has only left child
    if (pp == 0) m_root = p->m_left;
    else if (pp->m_left == p) pp->m_left = p->m_left;
    else pp->m_right = p->m_left;

    delete p;
    return;
}

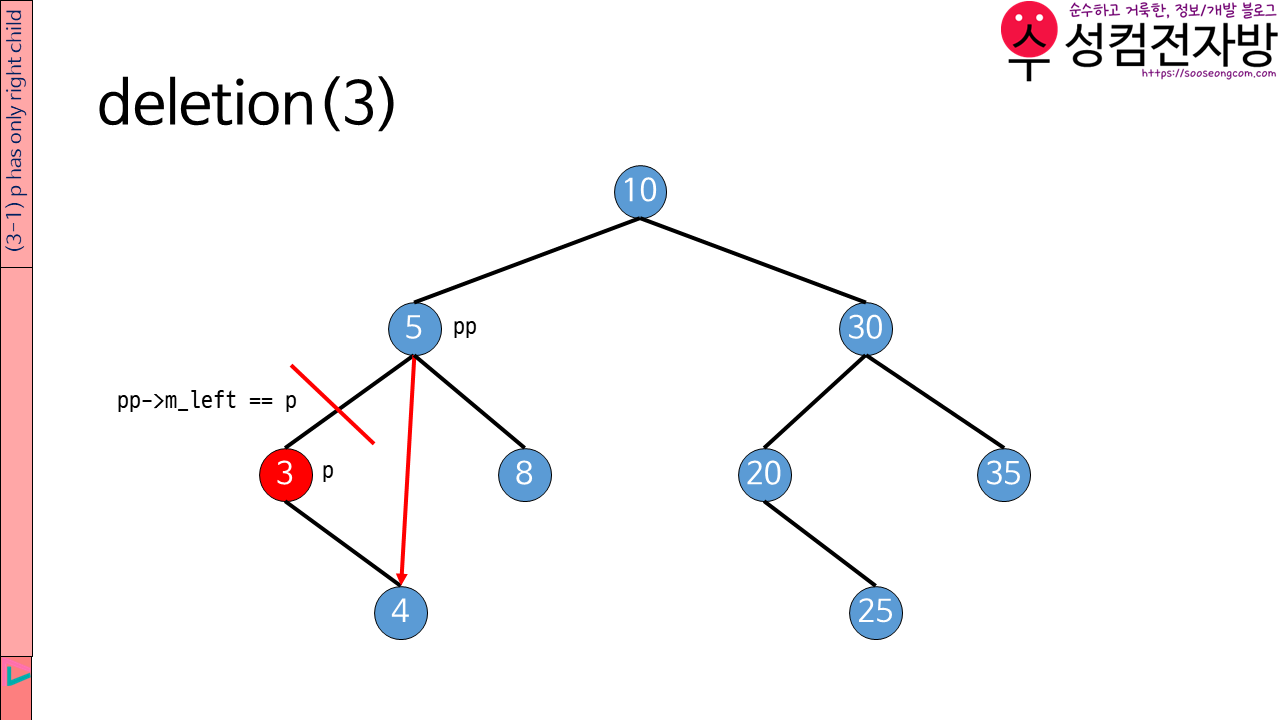
p has only left child
p의 자식 node가 1개일 경우 p가 right child를 갖는지 left child를 갖는지에 따라 나누어 작동합니다. 위의 이미지는 p가 right child를 갖는 예시입니다. 위의 예시에서 p가 pp의 left child이므로 pp의 left child를 p의 right child에 연결합니다.

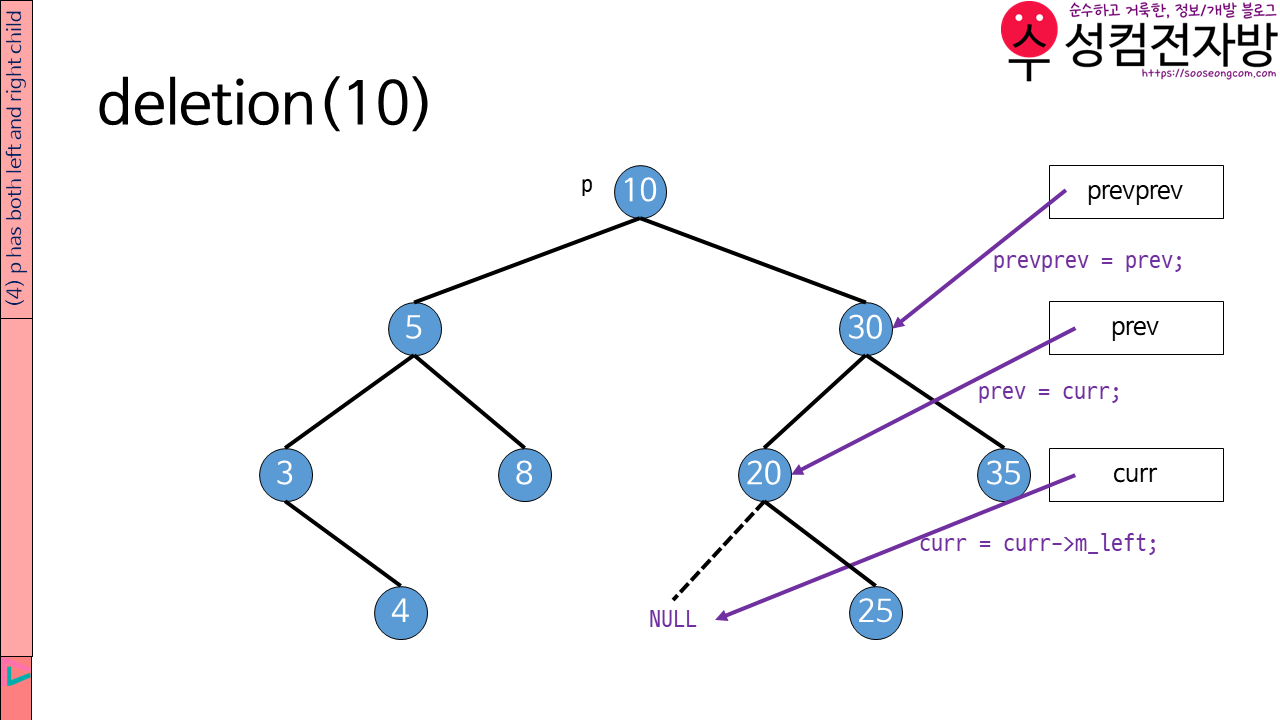
4.4. if p is a degree 2 node (p has both left and right child)

//(4) p has both left and right child
TreeNode<T>* prevprev = p, * prev = p->m_right, * curr = p->m_right->m_left;

while (curr) {
    prevprev = prev;
    prev = curr;
    curr = curr->m_left;
}

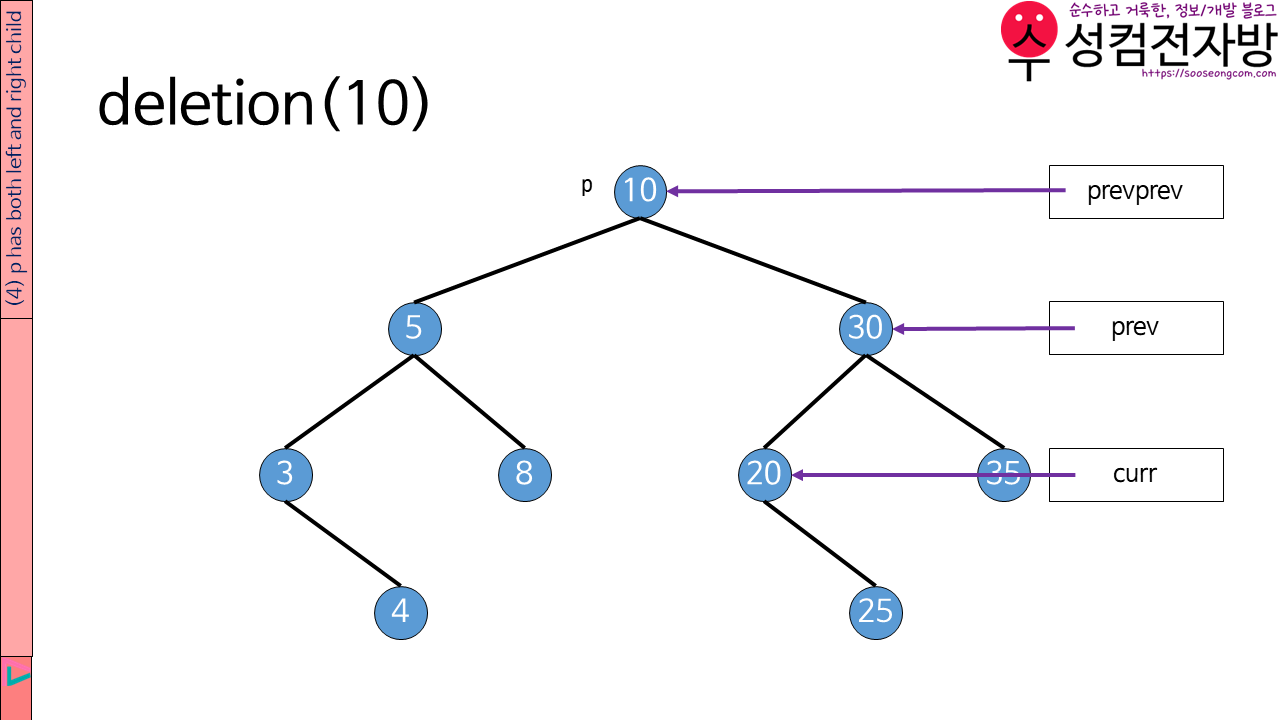
p has both left and right child take-1
처음에는 prevprev를 p에, prev를 p->m_right에, curr를 p->m_right->m_left에 연결합니다.

p has both left and right child take-2
그 다음 while문을 통해 curr이 NULL이 될 때까지 자식 node로 내려갑니다.

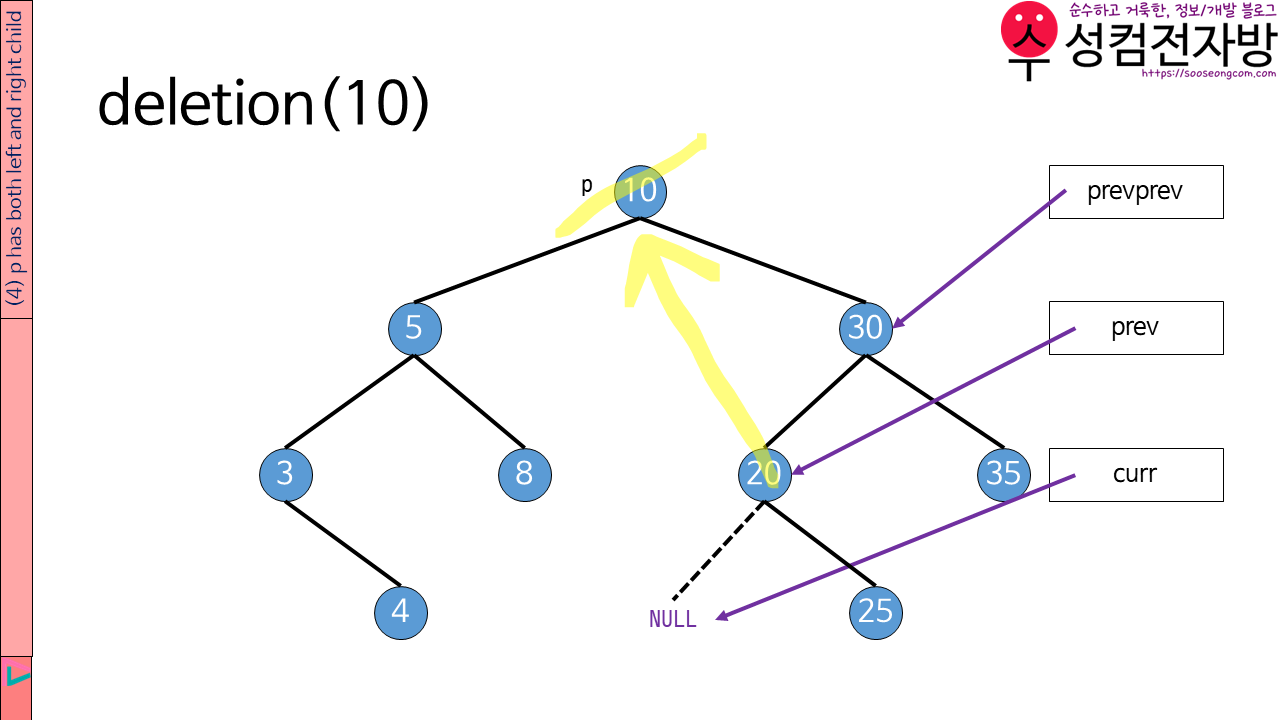
/* now, curr == 0
 * prev is the node to be deleted
 * prevprev is prev's parent
 * prev->m_left==0
 */

now, curr is equal to 0
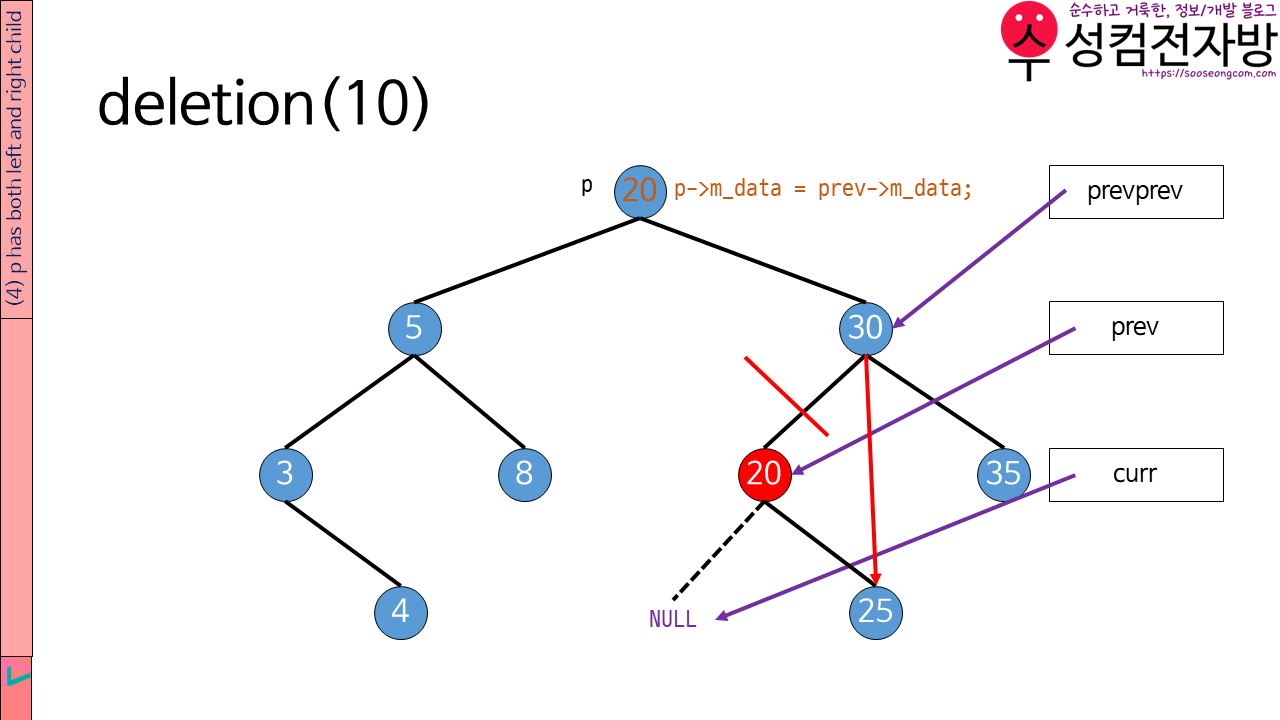
node p는 left subtree의 가장 큰 node 또는 its right subtree의 가장 작은 node로 대체되어야 합니다. 제 소스코드에서는 node p는 left subtree의 가장 큰 node로 대체됩니다. prev의 data는 p로 옮겨질 것입니다. 그 다음 prev를 삭제합니다.

    p->m_data = prev->m_data;
	if (prevprev == p) prevprev->m_right = prev->m_right;
	else prevprev->m_left = prev->m_right;
	delete prev;
	return;
}

delete 20

5. operator<< overloading

BinarySearchTree 객체 BST가 있을 때 cout << BST는 cout << BST.m_root을 실행합니다.
TreeNode 객체 treenode가 있을 때, cout << treenode는 root가 treenode인 Binary Search Tree를 출력합니다.

//BinarySearchTree.h Line 23~30
friend std::ostream& operator<<(std::ostream& os, const BinarySearchTree<T>& tree) {
    //InOrder
    TreeNode<T>* t = tree.m_root;

    os << t;

    return os;
}

//TreeNode.h Line 28~49
friend std::ostream& operator<<(std::ostream& os, const BinarySearchTree<T>& tree) {
    //InOrder
    TreeNode<T>* t = tree.m_root;

    os << t;

    return os;
}

TreeNode.h에서 operator<<()는 InOrder Traversal을 수행합니다.

6. 소멸자(destructor)

소멸자는 BinarySearchTree<T>::deletePostOrder(TreeNode<T>* t)를 호출합니다. BinarySearchTree<T>::deletePostOrder(TreeNode<T>* t)는 InOrder Traversal을 수행합니다.

template <class T>
void BinarySearchTree<T>::deletePostOrder(TreeNode<T>* t) {
	if (t != NULL) {
		deletePostOrder(t->m_left);
		deletePostOrder(t->m_right);
		delete t;
	}
}

template <class T>
BinarySearchTree<T>::~BinarySearchTree() {
	deletePostOrder(m_root);
}

7. template class를 friend 선언하는 방법

//TreeNode.h Line 6~10, 49
template <class T>
class TreeNode
{
	template <class U>
	friend class BinarySearchTree;
private:
//...
}

TreeNode도 template으로 되어 있습니다. TreeNode.h에서 TreeNode의 template parameter(매개변수)로 T를 사용했습니다. 그 안에서 BinarySearchTree를 friend 선언하기 위해서는 T 말고 다른 parameter를 사용해야 합니다.

template <class U>
friend class BinarySearchTree;

이렇게 써 주면 BinarySearchTree의 자료형과 상관없이 friend 선언이 됩니다.

8. 글 마무리

이 글에서 설명하지 않은 부분(class 생성자 등)은 제가 GitHub에 올려 둔 소스코드(https://github.com/sooseongcom/BinarySearchTree.git)를 참고하시기 바랍니다. 제 글을 읽어 주셔서 감사합니다. 다음에 만나요!

9. Reference

1) Pubby. 2012. “Class template with template class friend, what’s really going on here?”, stackoverflow. (2024. 01. 01. 방문). https://stackoverflow.com/questions/8967521/class-template-with-template-class-friend-whats-really-going-on-here

필자(수성컴)의 노트북은 갤럭시 북 Flex2입니다.(Windows 11)

목차