진리표(truth table)를 보고 boolean equation을 만들 때 변수가 4개 이하이면 Karnaugh Map을 이용할 수 있습니다. 그러나 변수가 5개 이상으로 늘어나면 Karnaugh Map을 사용하기 힘들어집니다. 그러므로 Quine-McCluskey Algorithm을 사용하면 변수 개수가 많아도 boolean equation을 쉽게 도출할 수 있게 됩니다. 다만, Quine-McCluskey Algorithm은 사람이 직접 수행하기에 따분한 작업이므로 자동화 프로그램을 만들었습니다.
목차
1. 사용자 설명서
1.1. 시스템 요구사항
1.2. 파일 내려받기
1.3. 프로그램 사용법
1.4. Qunie-McCluskey Algorithm이란?
2. 개발자 설명서
2.1. How To Build
2.2. Files
2.3. Implicant Table Column 1 (Step 1)
2.4. Combining variables (Step 2~3)
2.5. Construct a PI table (Step 4)
2.6. Identify essential PIs (Step 5~6)
2.7. Find minimum set of PIs(Petrick’s Method) (Step 7)
2.8. Cost (# of transistors)
1. 사용자 설명서
1.1. 시스템 요구사항
- 운영체제: Windows
- 아키텍처: x64(AMD64, Intel64)
1.2. 파일 내려받기
1.2.1. https://github.com/sooseongcom/Quine-McCluskey?tab=readme-ov-file#12-download로 접속하셔서 본인 PC에 맞는 버전의 설치 파일을 내려받습니다.
1.2.2. 웹 브라우저(MS Edge 기준)에서 차단 경고가 뜰 경우 ··· 클릭 후 유지를 클릭합니다.
1.2.3. 더 보기 v를 클릭합니다.
1.2.4. 그래도 계속을 클릭합니다.
1.2.5. 그러면 설치 파일을 내려받으실 수 있습니다. 내려받으신 후 실행합니다.
1.2.6. Windows에서 SmartScreen 경고가 뜰 경우 추가 정보 클릭 후 실행을 클릭합니다.
1.3. 프로그램 사용법
1.3.1. 실행 파일이 있는 경로(예: Windows의 경우 exe 파일이 있는 폴더와 같은 폴더)에 input_minterm.txt를 생성합니다.
1.3.2. 예를 들어 설명해 드리겠습니다. f(A, B, C, D)=Σm(0, 1, 2, 5, 7, 10, 12, 13)+Σd(3, 8, 15)를 구하려면 input_minterm.txt의 내용은 아래와 같습니다.
4
m 0000
m 0001
m 0010
d 0011
m 0101
m 0111
d 1000
m 1010
m 1100
m 1101
d 1111
[Line 1]
첫 줄 숫자는 input bit length를 나타냅니다.
[Line 2]
m 0000
둘째 줄부터는 true minterm인지 don’t care minterm인지 구분하는 문자와 minterm 값(implicant)을 작성합니다.
m은 true minterm을, d는 don’t care minterm을 나타냅니다.
1.3.3. 실행 파일(Quine-McCluskey-Algorithm-버전.exe)을 실행합니다.
1.3.4. result.txt를 확인합니다.
-0-0
110-
0--1
Cost (# of transistors): 28
[Line 1~3]
이 term들은 결과적으로 나온 essential Prime Implicant입니다. 이것들을 조합하면
\(f(A, B, C, D)=\bar{B}\bar{D}+AB\bar{C}+\bar{A}D\)
가 됩니다.
그러나 실제로는 보통 bubble pushing을 하여 NAND Gate를 사용하실 테니 모든 gate를 NAND로 사용하시면 되겠습니다.
[Line 5]
Cost는 트랜지스터 개수입니다. Bubble pushing을 고려하여 계산된 결과입니다.
1.4. Qunie-McCluskey Algorithm이란?
Qunie-McCluskey Algorithm은 logic function을 minimize하기 위한 tabular algorithm입니다.
예제로 f(A, B, C, D)=Σm(0, 1, 2, 5, 7, 10, 12, 13)+Σd(3, 8, 15)를 사용하겠습니다.
f(A, B, C, D)는 boolean equation의 변수가 A, B, C, D라는 뜻입니다.
Σm(0, 1, 2, 5, 7, 10, 12, 13)은 0, 1, 2, 5, 7, 10, 12, 13이 true minterm이라는 뜻입니다.
Σd(3, 8, 15)는 3, 8, 15가 don’t care minterm이라는 뜻입니다.
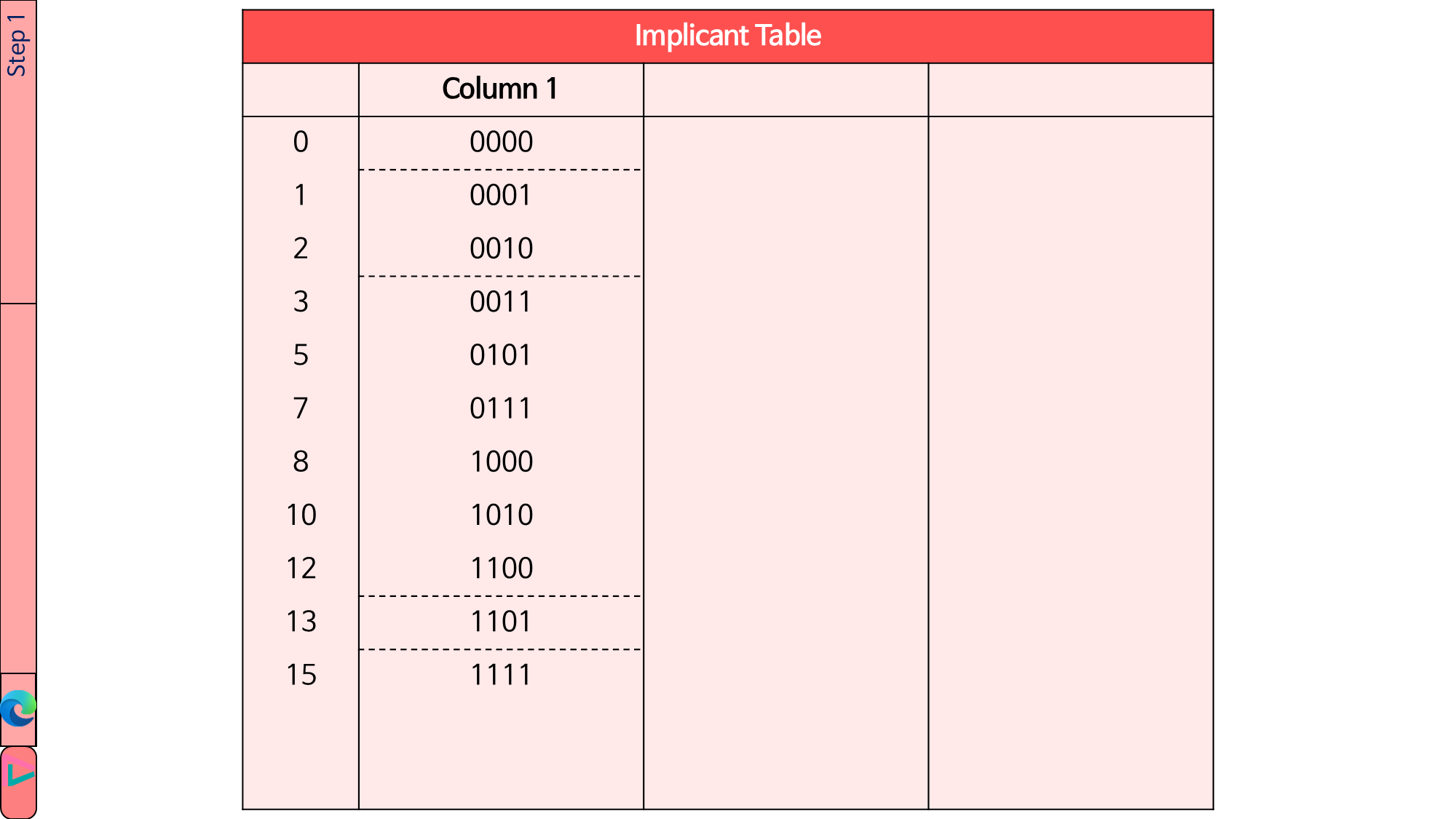
1.4.1. true minterm들과 don’t care minterm들을 Implicant table의 Column 1에 작성합니다. 이때 1의 개수에 따라 그룹을 나눕니다.
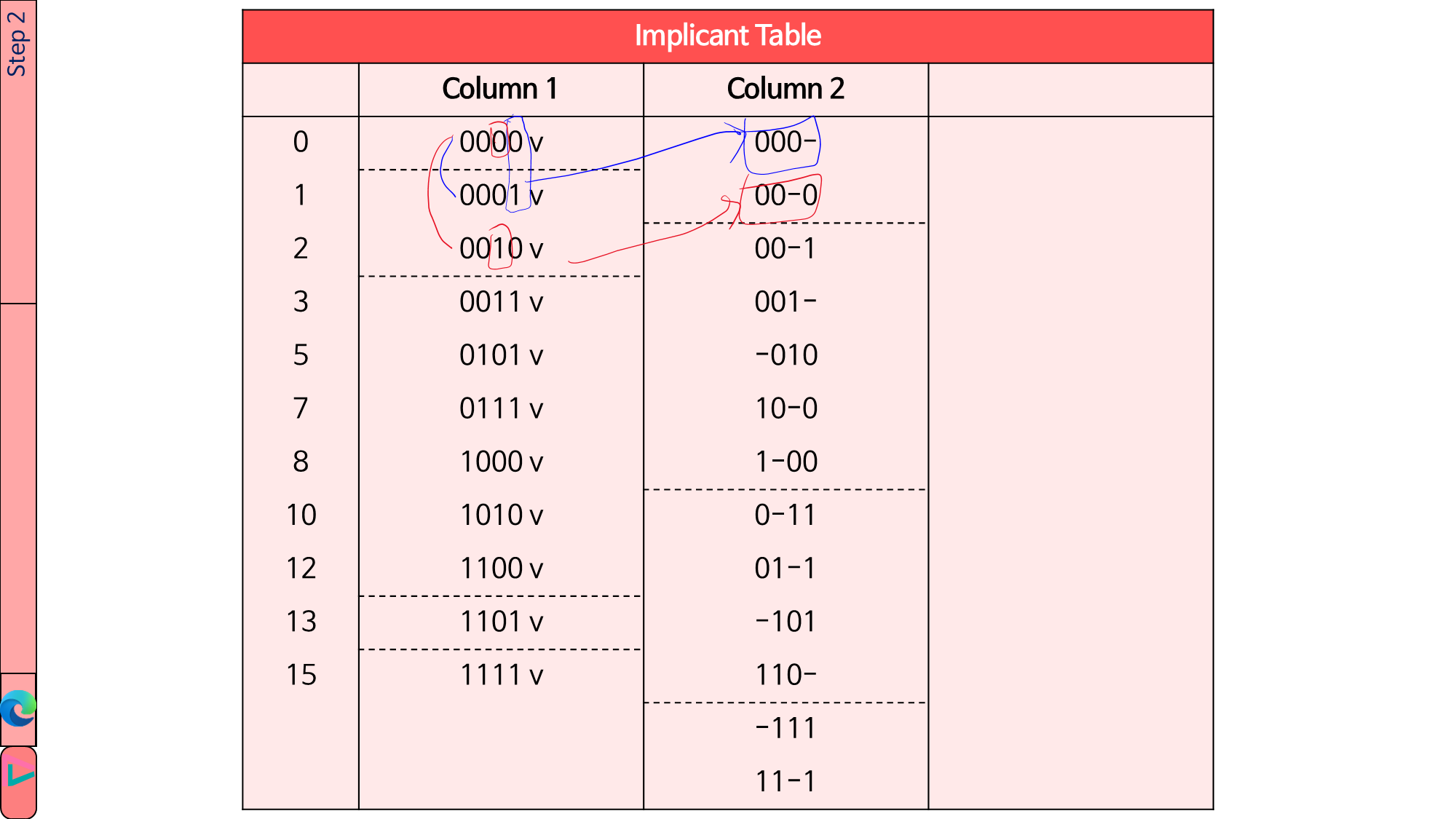
1.4.2. 인접한 두 그룹에서 Hamming distance가 1이 되도록 minterm을 하나씩 고릅니다. 변수가 다른 자리는 ‘-‘로 바꾸어 Column 2에 작성합니다. ‘-‘는 don’t care를 의미합니다. Column 1→2로 합쳐진 minterm은 Column 1에서 v 표시를 합니다. 이러한 과정을 모든 변수에 대해서 진행합니다.(v 표시가 되었다고 해서 더 이상 안 보는 것이 아니라, 두 그룹을 비교할 때는 모든 변수에 대해서 확인해야 합니다.) Column 1의 모든 변수를 순회했음에도 v 표시가 되지 않은 것은 * 표시를 합니다.
예1) 0000과 0001 → 000-
예2) 0000과 0010 → 00-0
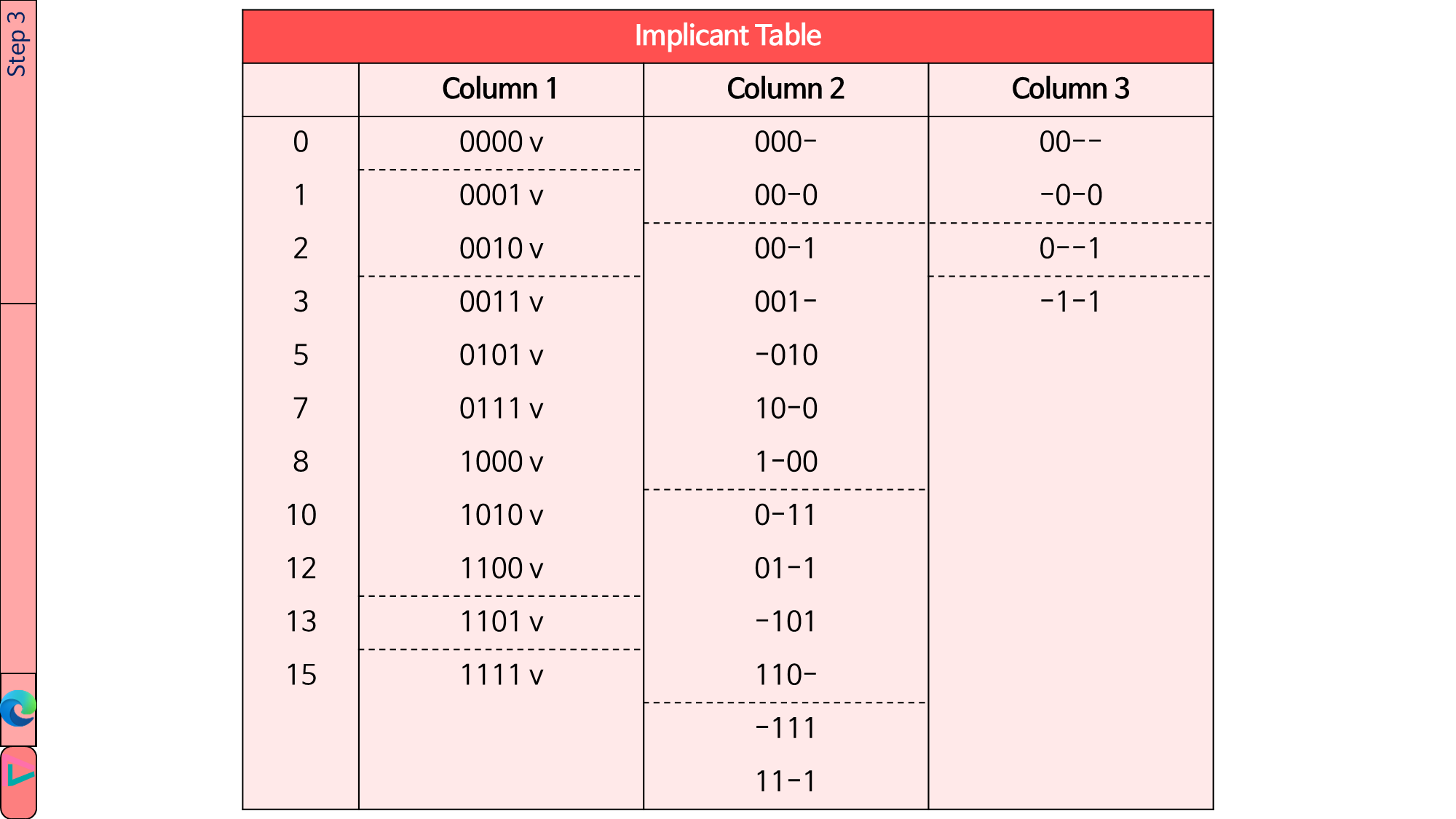
1.4.3. 앞에서 한 것처럼 Column 2의 implicant들을 합쳐서 Column 3에 작성합니다. 이때 ‘-‘가 있으면 ‘-‘의 자리는 일치해야 합니다. Column N의 implicant들을 합쳐서 Column N+1에 작성하기를 모든 implicant들이 v 또는 * 표시가 될 때까지(즉, 더 이상 combining을 할 수 없을 때까지) 진행합니다.
이제 * 표시가 된 implicant들이 prime implicant가 됩니다.
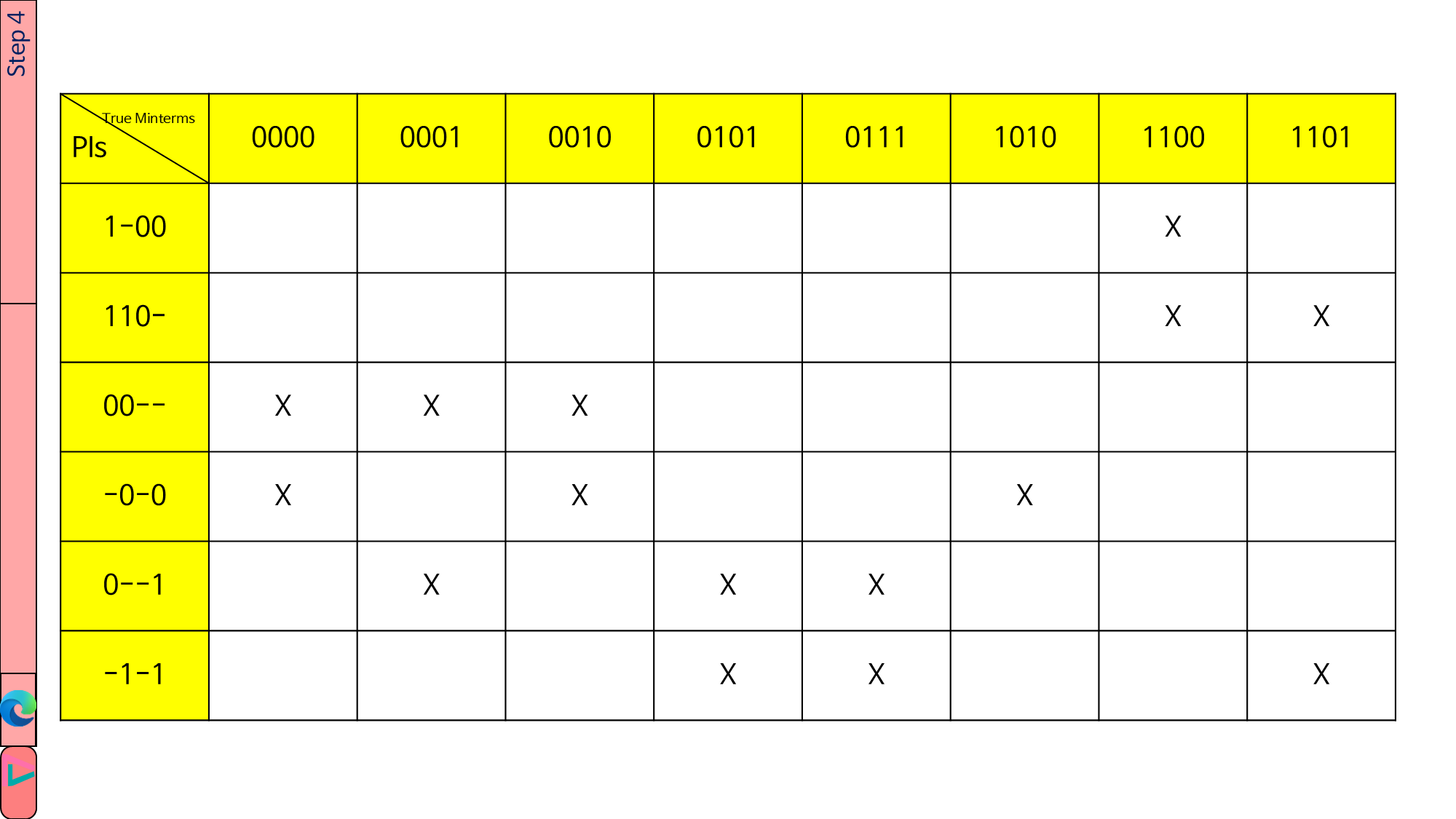
1.4.4. PI table을 만듭니다.
- 열: true minterms
- 행: PIs
PI가 minterm을 cover하는 곳에 ‘X’ 표시합니다.
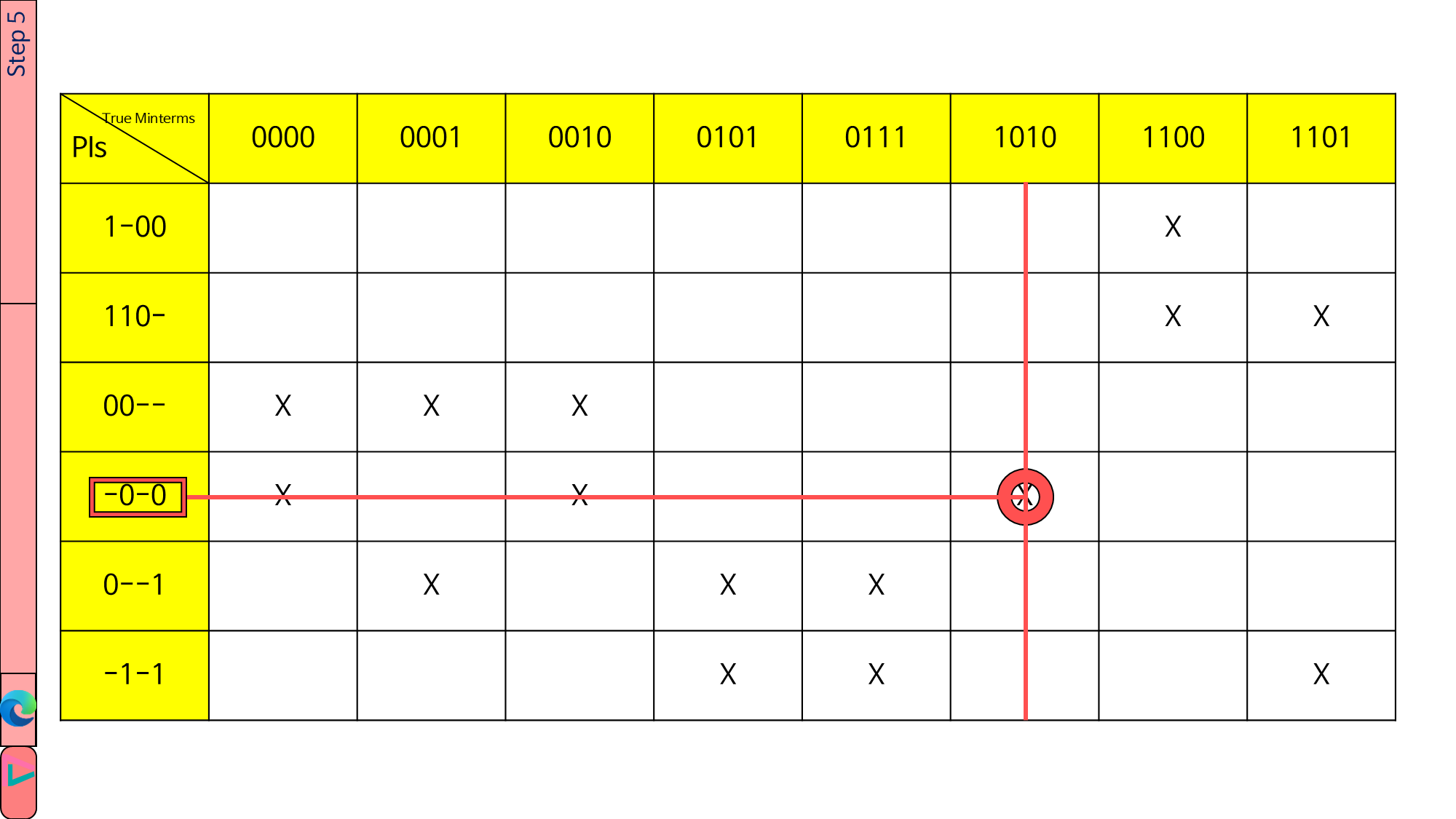
1.4.5. 이제 essential PI를 찾을 것입니다.
‘X’가 1개밖에 없는 열을 찾습니다. 예제에서는 True Minterms가 1010인 열이군요.
그 열의 ‘X’를 동그라미 합니다. 그리고 그 ‘X’를 기준으로 세로줄과 가로줄을 긋습니다.
예제에서는 가로줄이 -0-0에 닿았습니다. -0-0이 essential PI가 됩니다.
참고) 만약 ‘X’가 1개밖에 없는 열이 여러 개 있으면 essential PI가 여러 개 나올 것입니다.
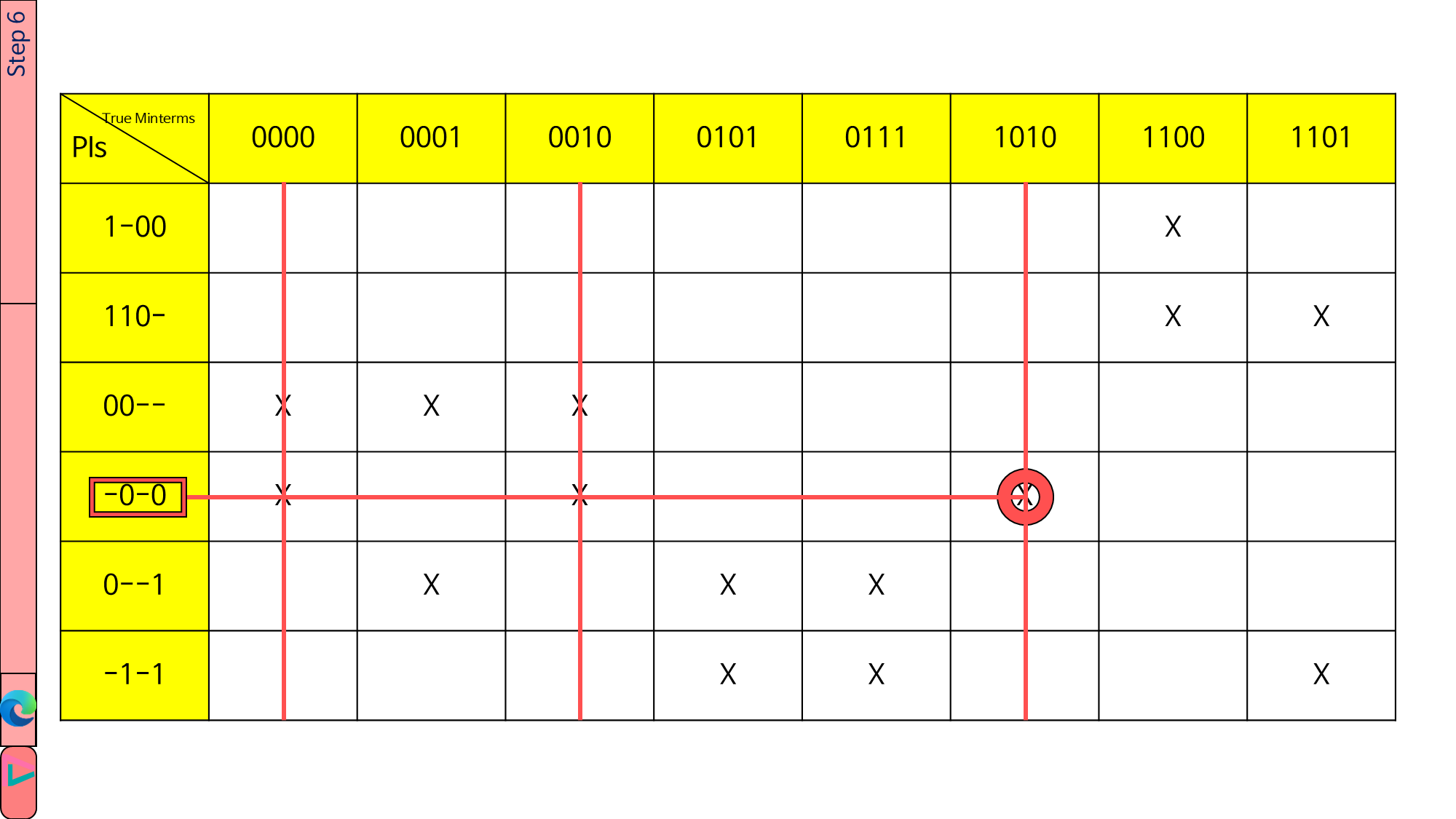
1.4.6. essential PI에 의해 cover되는 열들을 지울 것입니다. 가로줄 위에 있는 ‘X’에서 각각 세로줄을 그어 주면 됩니다.
어떨 때는 이 과정까지 하고 나면 모든 ‘X’들이 지워져서 최종 식이 도출되지만, 오늘의 예제는 ‘X’가 남게 되었습니다. 그러므로 남은 ‘X’들끼리 PI table을 새로 만들어 주겠습니다.
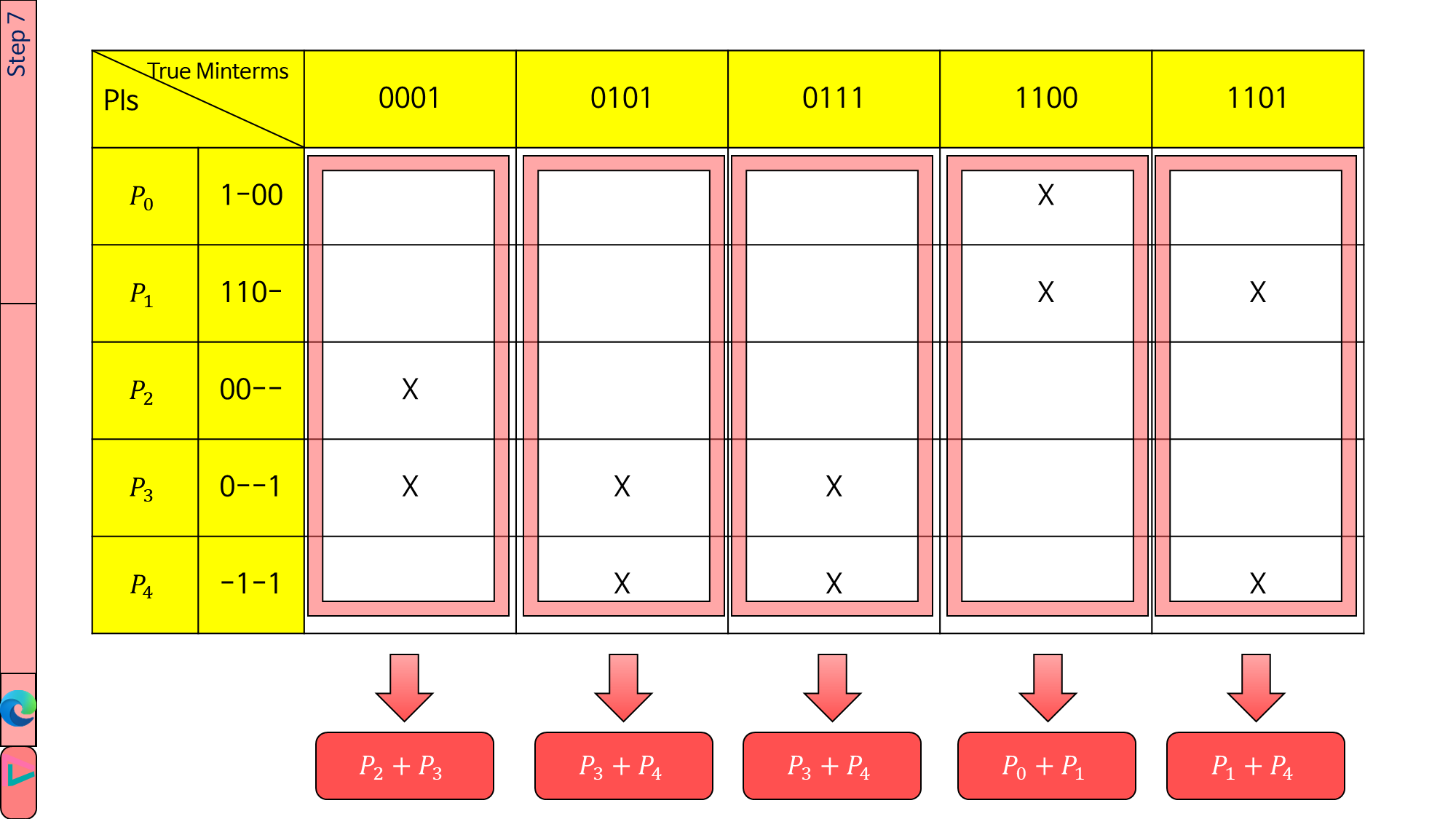
1.4.7. 이것이 새로 만든 PI table입니다. 열들을 보니 모든 열에 ‘X’가 2개씩 있습니다.
이때는 Petrick’s Method를 사용합니다.
편의상 PI마다 \(P_0\)부터 \(P_4\)까지 기호를 매겨 주었습니다.
그러면 이 PI table의 모든 ‘X’를 cover하는 식은 \(P=(P_2+P_3)(P_3+P_4)(P_0+P_1)(P_1+P_4)\)가 됩니다.
전개하면
\(\begin{align}
P &= (P_2+P_3)(P_3+P_4)(P_0+P_1)(P_1+P_4) \\
&= (P_3 + P_2 P_4)(P_1 + P_0 P_4) \\
&= P_1 P_3 + P_0 P_3 P_4 + P_1 P_2 P_4 + P_0 P_2 P_4
\end{align}\)
가 됩니다.
이것 중에서 PI 개수가 가장 적은 항인 \(P_1 P_3\)을 택합니다.
만약 PI 개수가 가장 적은 항이 여러 개라면 트랜지스터 개수를 비교하여 가장 저렴한 것을 택합니다.
2. 개발자 설명서
2.1. How To Build
(추후 작성 예정)
2.2. Files
- .gitignore: Git add 시 x64(folder), *.vcxproj, *.vcxproj.filters, *.vcxproj.user, input_minterm.txt, result.txt를 제외
- ImpTable.cpp: ImpTable의 멤버 함수/변수
- ImpTable.h: implicant table를 위한 class
- LICENSE: MIT License
- main.cpp: main function
- Minterm.cpp: Minterm의 멤버 함수/변수
- Minterm.h: implicant table을 위한 minterm을 위한 class
- PetrickTable.cpp: PetrickTable의 멤버 함수/변수
- PetrickTable.h: Petrick’s Method를 위한 PI Table
- PITable.cpp: PITable의 멤버 함수/변수
- PITable.h: PI Table를 위한 class
2.3. Implicant Table Column 1 (Step 1)
Implicant Table은 ImpTable class에서 담당합니다.
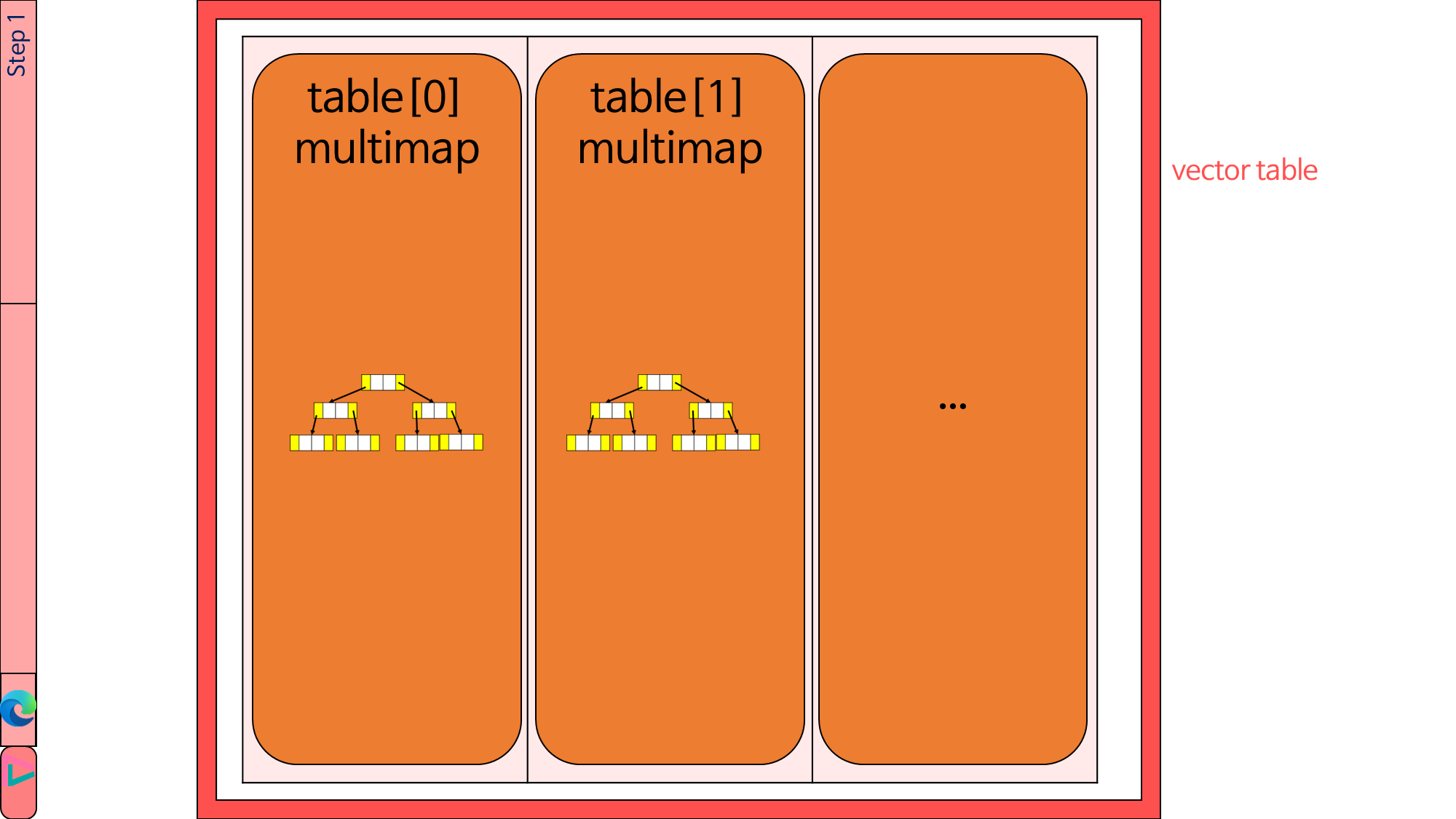
전체 implicant table의 자료형은 vector입니다.
table의 각 원소는 multimap입니다.
multimap의 key는 1의 개수이고, value는 implicant입니다.
//ImpTable.h Line 13~18
/** the type of table
* vector
* multimap<int, Minterm*>*: vector 확장 시 multimap을 재생성하므로 dynamic allocation해야 함.
* Minterm*: 생성 편의를 위해 dynamic allocation해야 함.
*/
vector<multimap<int, Minterm*>*> table;
2.4. Combining variables (Step 2~3)
Step 2~3는 int ImpTable::combine(int a) 함수가 공통적으로 담당합니다. a는 implicant table의 column 번호입니다. int ImpTable::combine(int a) 함수는 combining에 성공하면 1을, 아무것도 combining하지 못하면 0을 return합니다.
//main.cpp Line 34~38
//Step 2~3
for (int i = 0; combined == 1; i++) {
combined = imp_table->combine(i);
}
pi = imp_table->getPI();
따라서 위 코드와 같이 함수의 return 값이 0이 될 때까지 for문을 돌려 주면 PI를 구할 수 있습니다.
Minterm의 멤버 변수 marked의 초기 값은 0입니다.
v 표시를 하는 경우 Minterm의 멤버 변수 marked를 1로 설정합니다.
모든 combining 과정을 마친 후에도 marked가 0인 Minterm이 stared(*) minterm입니다.
2.5. Construct a PI table (Step 4)
PI table은 PITable class에서 담당합니다.
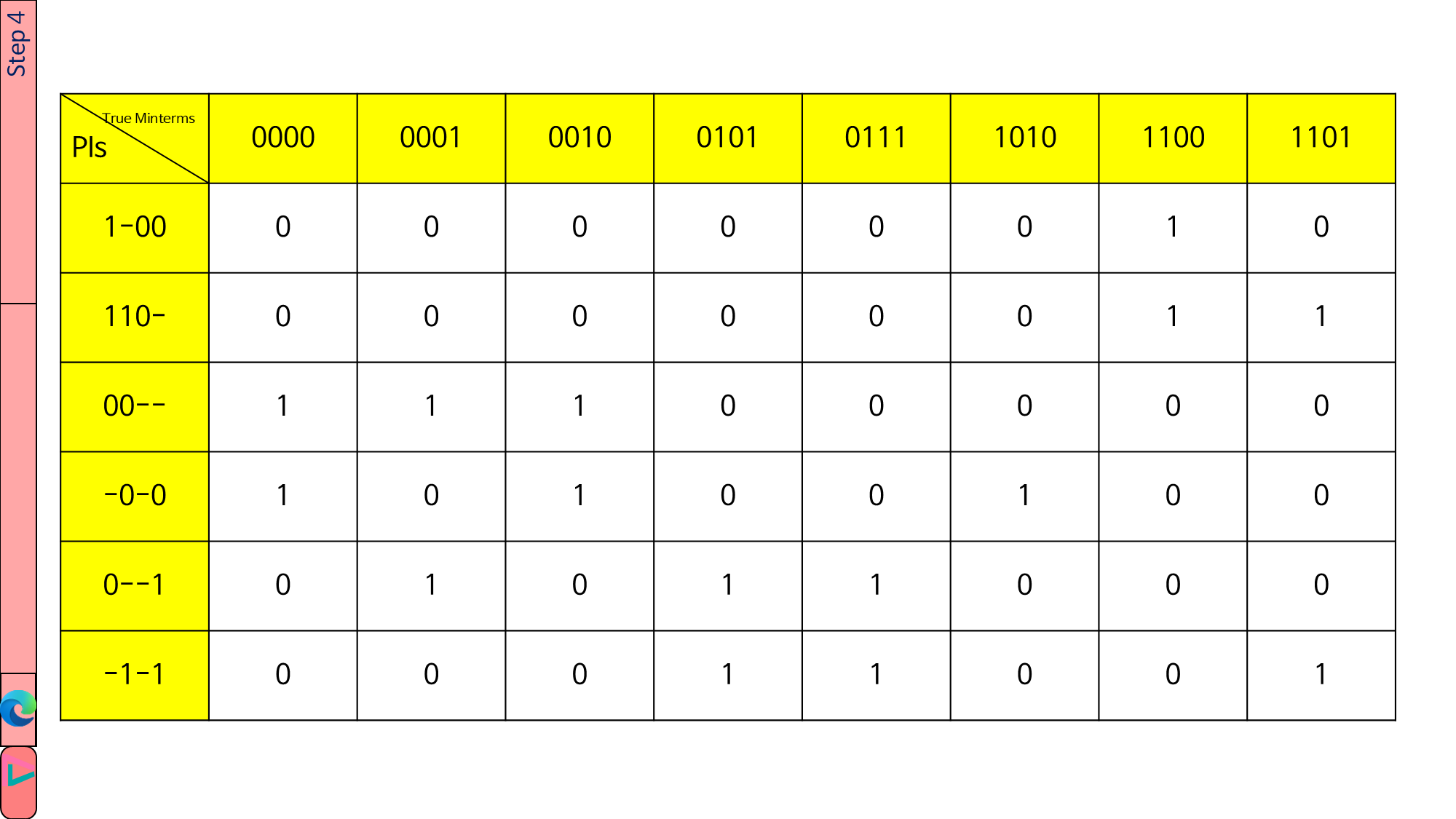
PI table은 2차원 vector로 만듭니다. vector<vector<int>>로 선언할 것이며, 위의 이미지에서 흰색 칸만 만들었습니다.
//PITable.cpp Line 3~12
PITable::PITable(vector<string> inpPI, vector<string> inpTM) {
/**
* Row: PIs
* Column: true minterms
*
* -1: deleted
* 0: blank
* 1: PI covers the minterm
* 2: only 1 in the column
*/
vector는 선언하면 0으로 초기화됩니다.
//PITable.cpp Line 129~137
int piCoverTm(string inpPI, string inpTM, int length) {
for (int i = 0; i < length; i++) {
if (inpPI[i] != '-' && inpPI[i] != inpTM[i]) {
return 0;
}
}
return 1;
}
PI가 minterm을 cover하는 곳에 1을 넣습니다.
2.6. Identify essential PIs (Step 5~6)
Step 5~6는 int PITable::identifyEPI() 함수가 담당합니다.
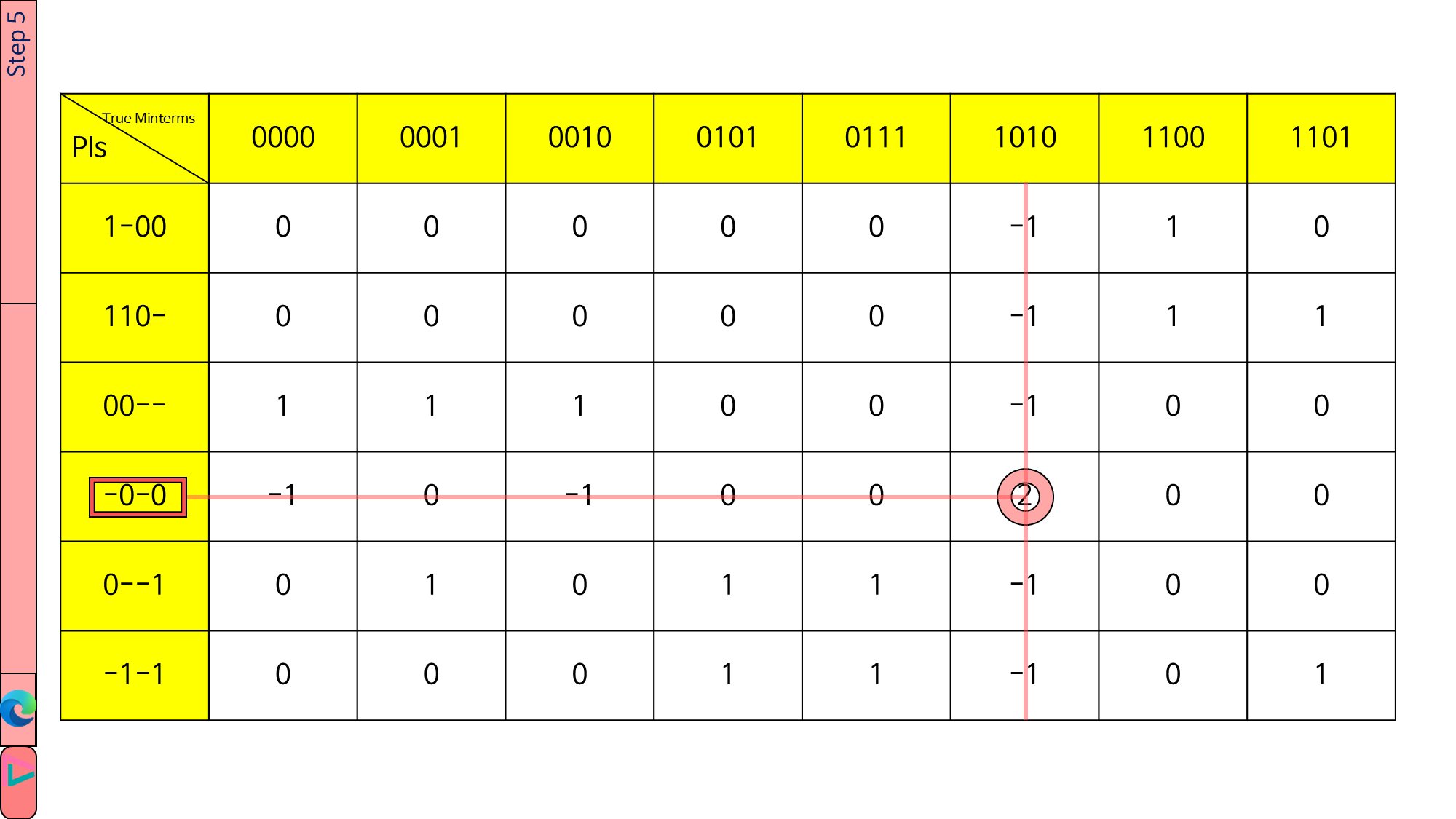
1이 1개밖에 없는 열을 찾습니다. 예제에서는 True Minterms가 1010인 열입니다.
그 열의 1을 2로 바꿉니다(빨간 동그라미를 쳤다는 뜻). 그리고 그 1을 기준으로 세로줄과 가로줄을 긋습니다. 세로줄은 모두 -1로 바꾸고, 가로줄은 1만 -1로 바꿉니다.
예제에서는 가로줄이 -0-0에 닿았습니다. -0-0가 epi에 없는지 확인하고 없다면 push합니다.
1이 1개밖에 없는 열을 찾을 때마다 complete이라는 변수를 1 증가시킵니다.
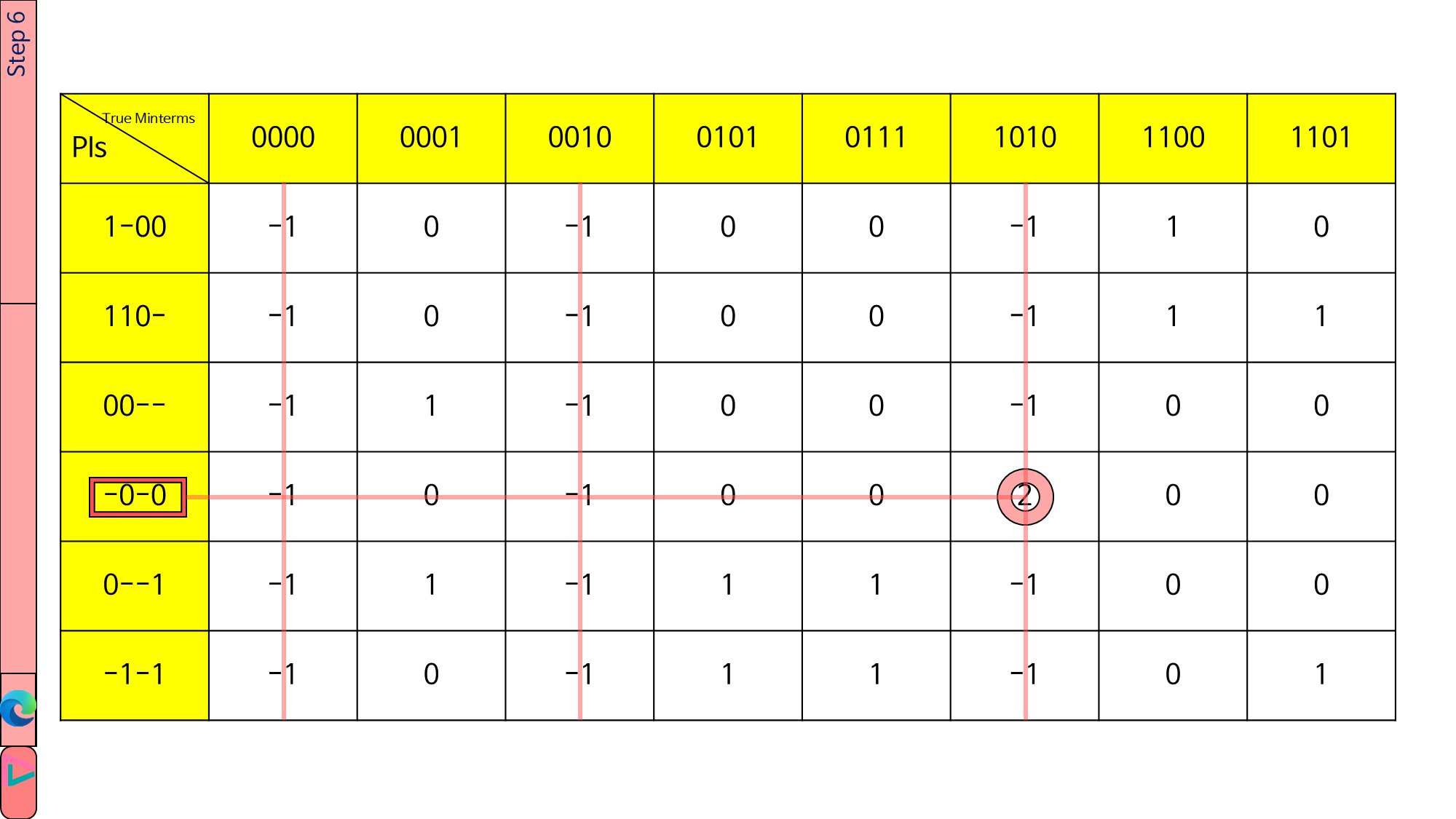
가로줄의 1을 -1로 바꿀 때 그 -1이 있는 열을 -1로 바꿉니다(단, 2는 그대로 유지). 그때마다 complete을 1씩 증가시킵니다.
int PITable::identifyEPI() 함수는 tm.size() - complete을 return합니다.
모든 열이 지워진 상태라면 return 값은 0이 될 것입니다.
1이 남아 있는 열이 있다면 return 값은 0보다 클 것이며, Step 7을 진행해야 합니다.
2.7. Find minimum set of PIs(Petrick’s Method) (Step 7)
Petrick’s Method를 위한 PI table을 새로 만들어야 하는데, 이는 PetrickTable class에서 담당합니다.
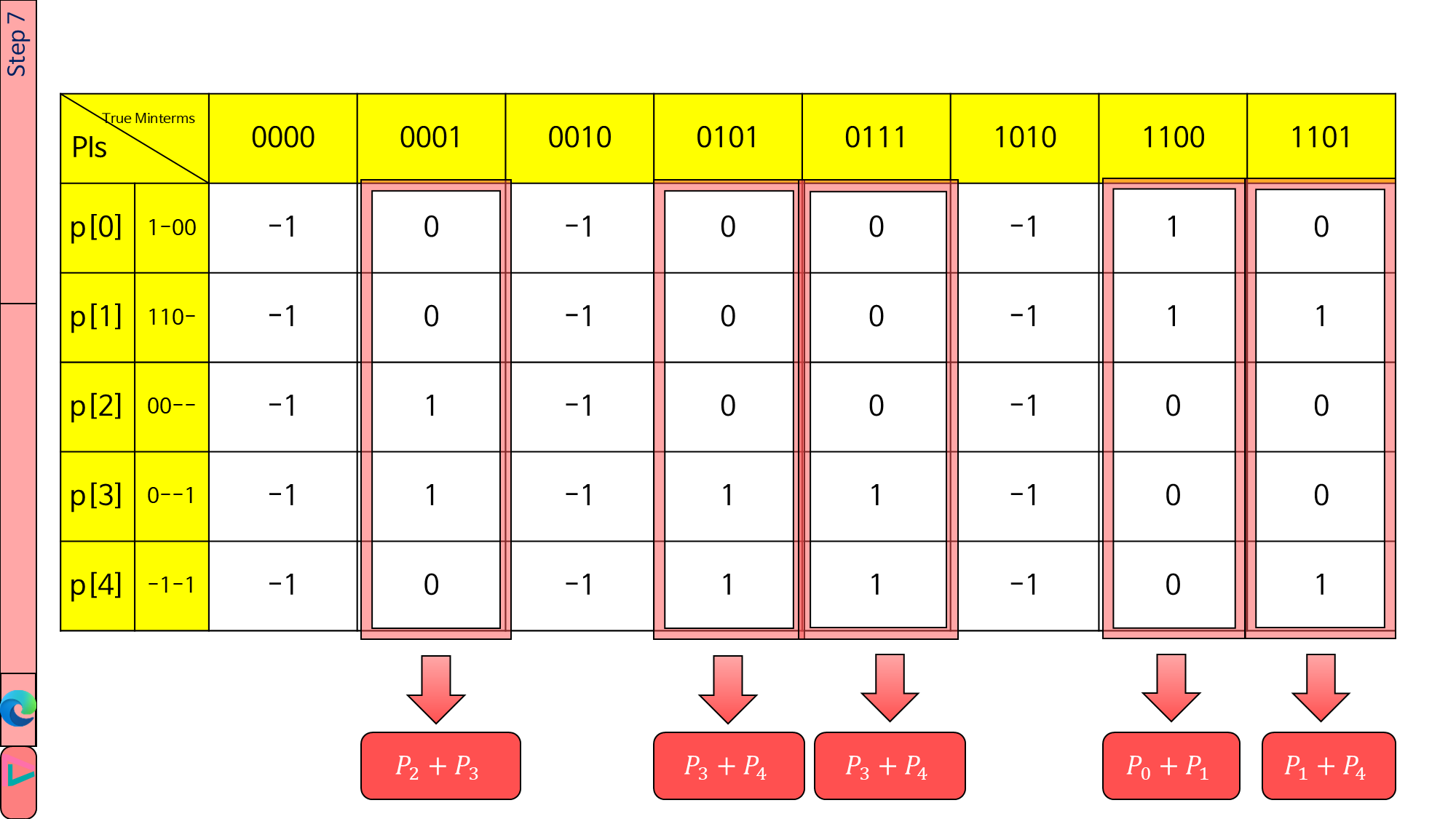
구조는 PITable과 유사합니다. True Minterms는 -1만 있는 열이 있어도 무시하면 그만이기에 그냥 남겨 두었습니다. 다만, PI는 essential PI가 포함되면 식 도출할 때 오류가 발생할 수 있기에 삭제해 주었습니다.
이제 여기서 식을 어떻게 도출할 것이냐가 문제입니다. 일단 식은 \(P=(P_2+P_3)(P_3+P_4)(P_0+P_1)(P_1+P_4)\)로 잘 나옵니다.
다만, 이것을 전개하기가 어려우므로 \(P_0\)부터 \(P_4\)까지를 int형 p[0]부터 p[4]로 동적 할당했습니다.
- 전체 식:
vector<set<int*>> - 각 괄호:
set<int*> - 괄호 안의 각 항: int*
p[0]부터 p[4]까지를 0 또는 1을 넣어 보면서 전체 식 결과가 1이 되는 조합을 찾습니다. 중복순열 알고리즘을 차용했습니다.
괄호 안에서는 여러 항 중 하나만 1이어도 그 괄호 전체가 1이 되므로 set 안에서 int 값이 1인 것이 있는지 찾아보면 됩니다.
전체 식은 괄호의 곱으로 연결되어 있어서 각 괄호가 모두 1이어야 전체 식의 결과도 1이 됩니다. 그러므로 모든 set 안에 int 값이 1인 것이 있는지 찾아봐야 합니다.
그렇게 전체 식이 1인 것을 찾으면 그 p 조합이 바로 minimum set of PIs의 후보가 됩니다.
minimum set of PIs의 후보 중에서는 PI 개수가 가장 적은 항을 택합니다.
만약 PI 개수가 가장 적은 항이 여러 개라면(PetrickTable.cpp Line 179~190 else문) 트랜지스터 개수를 비교하여 가장 저렴한 것을 택합니다(PetrickTable.cpp Line 195~231 int PetrickTable::cost(int* pterms) 함수).
2.8. Cost (# of transistors)
-0-0
110-
0--1
essential PI가 위와 같이 나왔다면 \(f(A, B, C, D)=\bar{B}\bar{D}+AB\bar{C}+\bar{A}D\)입니다. 언뜻 보면 AND, OR, NOT으로 구현하면 될 것 같지만 실제로는 NAND Gate를 이용하는 것이 더 저렴하기 때문에 bubble pushing을 합니다.
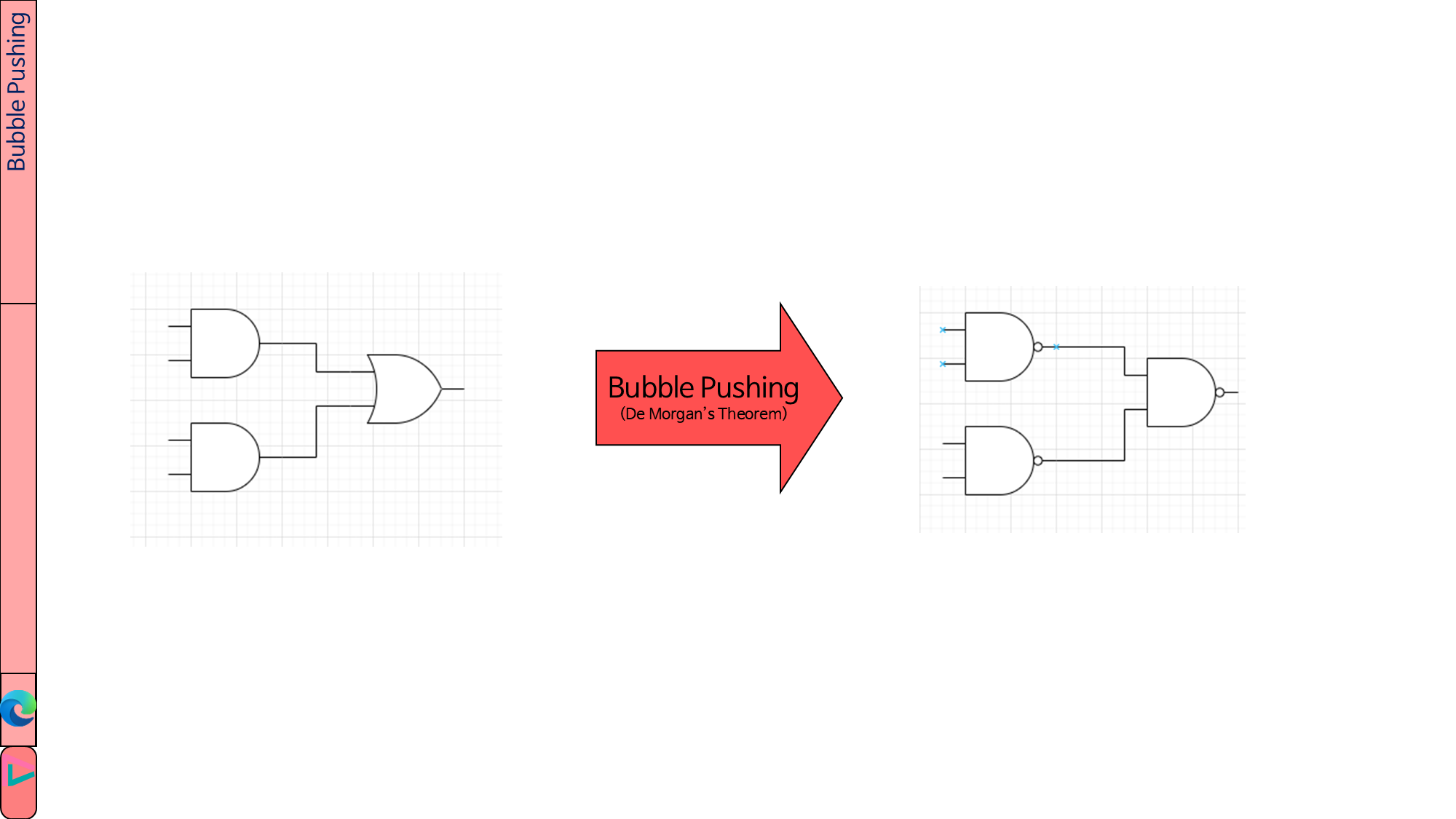
따라서 AND와 OR이 모두 NAND로 바뀐다고 생각하시면 됩니다.
- N-input NAND Gate의 트랜지스터 개수: 2N개
- NOT Gate의 트랜지스터 개수: 2개
3. 글 마무리
제 프로그램을 사용해 주셔서 감사합니다. 다음에 만나요!
4. 참고 자료
1) novs. 2022. “[C++] STL map vs multimap (feat. multimap equal_range)”, nov.Zip. (2025. 11. 28. 방문). https://novlog.tistory.com/entry/C-STL-map-vs-multimap-feat-multimap-equalrange
2) Jihan. 2023. “C++로 Quine-McCluskey 구현하기”, bbbjihan.log. (2025. 11. 28. 방문). https://velog.io/@bbbjihan/C로-Quine-McCluskey-구현하기
3) SCRIPTS BY. 2023. “vector VS list 뭘 써야 하지?”, SCRIPTS BY. (2025. 11. 28. 방문). https://nx006.tistory.com/20
4) BlockDMask. 2017. “[C++] multimap container 정리 및 사용법”, 가면 뒤의 기록. (2025. 11. 28. 방문). https://blockdmask.tistory.com/88
5) horang. n. d. “C++ std::string::erase 정리”, Code by horang. (2025. 11. 18. 방문). https://hoho325.tistory.com/317
6) BLASTIC. 2012. “[Quine-McCluskey Method] Petrick’s Method”, BLASTIC. (2025. 11. 18. 방문). https://blastic.tistory.com/204
7) 젠니. 2023. “[논리회로설계] Petrick’s Method”, Jenvelop log. (2025. 11. 18. 방문). https://velog.io/@tmdtmdqorekf/논리회로설계-Patricks-Method
8) 공부하는 식빵맘. 2020. “(C++) 중복 순열(Repeated Permutation) 구현하기”, 평생 공부 블로그 : Today I Learned. (2025. 11. 18. 방문). https://ansohxxn.github.io/algorithm/repeated-permutation/#google_vignette
9) Song 전자공학. 2025. “CMOS Logic Gates: CMOS 논리 게이트”, Song 전자공학. (2025. 11. 18. 방문). https://blog.naver.com/songsite123/223712874895
10) spring. 2020. “[c++] std::vector”, springkim.log. (2025. 11. 18. 방문). https://velog.io/@springkim/c-stdvector




